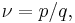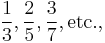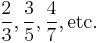Fractional quantum Hall effect
The fractional quantum Hall effect (FQHE) is a physical phenomenon in which the Hall conductance of 2D electrons shows precisely quantised plateaus at fractional values of 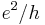 . It is a property of a collective state in which electrons bind magnetic flux lines to make new quasiparticles, and excitations have a fractional elementary charge and possibly also fractional statistics. Its discovery and explanation were recognized by the 1998 Nobel Prize in Physics.
. It is a property of a collective state in which electrons bind magnetic flux lines to make new quasiparticles, and excitations have a fractional elementary charge and possibly also fractional statistics. Its discovery and explanation were recognized by the 1998 Nobel Prize in Physics.
Contents |
Introduction
The fractional quantum Hall effect (FQHE) is a collective behaviour in a two-dimensional system of electrons. In particular magnetic fields, the electron gas condenses into a remarkable liquid state, which is very delicate, requiring high quality material with a low carrier concentration, and extremely low temperatures. As in the integer quantum Hall effect, a series of plateaus form in the Hall resistance. Each particular value of the magnetic field corresponds to a filling factor (the ratio of electrons to magnetic flux quanta)
where p and q are integers with no common factors. Here q turns out to be an odd number with the exception of two filling factors 5/2 and 7/2. The principal series of such fractions are
and
There were several major steps in the theory of the FQHE.
- Laughlin states and fractionally-charged quasiparticles: this theory, proposed by Laughlin, is based on accurate trial wave functions for the ground state at fraction
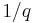 as well as its quasiparticle and quasihole excitations. The excitations have fractional charge of magnitude
as well as its quasiparticle and quasihole excitations. The excitations have fractional charge of magnitude 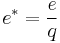 .
.
- Fractional exchange statistics of quasiparticles: Bertrand Halperin conjectured, and Daniel Arovas, J. R. Schrieffer, and Frank Wilczek demonstrated, that the fractionally charged quasiparticle excitations of the Laughlin states are anyons with fractional statistical angle
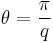 ; the wave function acquires phase factor of
; the wave function acquires phase factor of 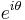 (together with an Aharonov-Bohm phase factor) when identical quasiparticles are exchanged in a counterclockwise sense.
(together with an Aharonov-Bohm phase factor) when identical quasiparticles are exchanged in a counterclockwise sense.
- Hierarchy states: this theory was proposed by Duncan Haldane, and further clarified by Halperin, to explain the observed filling fractions not occurring at the Laughlin states'
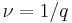 . Starting with the Laughlin states, new states at different fillings can be formed by condensing quasiparticles into their own Laughlin states. The new states and their fillings are constrained by the fractional statistics of the quasiparticles, producing e.g.
. Starting with the Laughlin states, new states at different fillings can be formed by condensing quasiparticles into their own Laughlin states. The new states and their fillings are constrained by the fractional statistics of the quasiparticles, producing e.g. 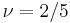 and
and 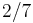 states from the Laughlin
states from the Laughlin 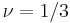 state. Similarly constructing another set of new states by condensing quasiparticles of the first set of new states, and so on, produces a hierarchy of states covering all the odd-denominator filling fractions. This idea has been validated quantitatively,[1] and brings out the observed fractions in a natural order. Laughlin's original plasma model was extended to the hierarchy states by MacDonald and others.[2]
state. Similarly constructing another set of new states by condensing quasiparticles of the first set of new states, and so on, produces a hierarchy of states covering all the odd-denominator filling fractions. This idea has been validated quantitatively,[1] and brings out the observed fractions in a natural order. Laughlin's original plasma model was extended to the hierarchy states by MacDonald and others.[2]
- Composite fermions: this theory was proposed by Jain, and further extended by Halperin, Lee and Read. The basic idea of this theory is that as a result of the repulsive interactions, two (or, in general, an even number of) vortices are captured by each electron, forming integer-charged quasiparticles called composite fermions. The fractional states of the electrons are understood as the integer QHE of composite fermions. For example, this makes electrons at filling factors 1/3, 2/5, 3/7, etc. behave in the same way as at filling factor 1, 2, 3, etc. Composite fermions have been observed, and the theory has been partially verified by experiment and computer calculations. Composite fermions are valid even beyond the fractional quantum Hall effect; for example, the filling factor 1/2 corresponds to zero magnetic field for composite fermions, resulting in their Fermi sea. Composite fermion theory provides a complementary description of the Laughlin and hierarchy states. It gives trial wave functions which, though not identical to those produced from the hierarchy picture (the wave functions for the Laughlin states are identical), are in the same universality class, as shown by Read. There are no experimental tests for fractional quantum Hall states that, even in principle, allow one to confirm the composite fermion description while excluding the hierarchy description.
The FQHE was experimentally discovered in 1982 by Daniel Tsui and Horst Störmer, in experiments performed on gallium arsenide heterostructures developed by Arthur Gossard. Tsui, Störmer, and Laughlin were awarded the 1998 Nobel Prize for their work.
Fractionally charged quasiparticles are neither bosons nor fermions and exhibit anyonic statistics. The fractional quantum Hall effect continues to be influential in theories about topological order. Certain fractional quantum Hall phases appear to have the right properties for building a topological quantum computer.
Evidence for fractionally-charged quasiparticles
Experiments have reported results that specifically support the understanding that there are fractionally-charged quasiparticles in an electron gas under FQHE conditions.
In 1995, the fractional charge of Laughlin quasiparticles was measured directly in a quantum antidot electrometer at Stony Brook University, New York.[3] In 1997, two groups of physicists at the Weizmann Institute of Science in Rehovot, Israel, and at the Commissariat à l'énergie atomique laboratory near Paris, detected such quasiparticles carrying an electric current, through measuring quantum shot noise.[4][5] Both of these experiments are somewhat controversial.
A more recent experiment,[6] which measures the quasiparticle charge extremely directly, appears beyond reproach.
The anyonic statistics, however, have neither been confirmed nor disproved by any of the experiments.
Impact of fractional quantum Hall effect
The FQH effect shows the limits of Landau's symmetry breaking theory. Previously it was long believed that the symmetry breaking theory could explain all the important concepts and essential properties of all forms of matter. According to this view the only thing to be done is to apply the symmetry breaking theory to all different kinds of phases and phase transitions. From this perspective, we can understand the importance of the FQHE discovered by Tsui, Stormer, and Gossard.
Different FQH states all have the same symmetry and cannot be described by symmetry breaking theory. Thus FQH states represent new states of matter that contain a completely new kind of order—topological order. The existence of FQH liquids indicates that there is a whole new world beyond the paradigm of symmetry breaking, waiting to be explored. The FQH effect opened up a new chapter in condensed matter physics. The new type of orders represented by FQH states greatly enrich our understanding of quantum phases and quantum phase transitions. The associated fractional charge, fractional statistics, non-Abelian statistics, chiral edge states, etc demonstrate the power and the fascination of emergence in many-body systems.
The explanation of this effect is open to new relations and interpretations of experiments in light of new theories. It is possible to consider that the FQHE really gives further evidence of the existence of magnetic flux quanta as detected in superconductivity. There are electromagnetic quanta of magnetic flux and electric elementary charge. It was shown that these fundamental quanta are determined by a physical geometric unified theory.[7] Each particle carries an integer charge and an integer flux. Classically, if a particle crosses a line in a plane normal to its flux, there is a fractional relation between the charge and flux crossing the line and a corresponding fractional relation between the current and induced voltage if there are no resistive losses. Quantum mechanically, the Hall effect problem may be treated by filling the quantum Landau energy levels produced by the presence of the magnetic field. The electrons carrying flux quanta may combine to form rotating systems or vortices which act as charge/flux carriers. It has been shown that the Hall electric conductivity is directly proportional to charge/flux ratios of these carriers.[8] Consequently, in accordance with the quantum aspects of the unified theory it is not necessary to assume the existence of fundamental fractional charges.
See also
- Laughlin wavefunction
- Hall probe
- Quantum Hall Effect
- Topological order
- Coulomb potential between two current loops embedded in a magnetic field
Notes
- ^ M. Greiter (1994). "Microscopic formulation of the hierarchy of quantized Hall states". Phys. Lett. B 336: 48. arXiv:cond-mat/9311062. Bibcode 1994PhLB..336...48G. doi:10.1016/0370-2693(94)00957-0.
- ^ A.H. MacDonald, G.C. Aers, M.W.C. Dharma-wardana (1985). "Hierarchy of plasmas for fractional quantum Hall states". Physical Review B 31 (8): 5529. Bibcode 1985PhRvB..31.5529M. doi:10.1103/PhysRevB.31.5529.
- ^ V.J. Goldman, B. Su (1995). "Resonant Tunneling in the Quantum Hall Regime: Measurement of Fractional Charge". Science 267 (5200): 1010. Bibcode 1995Sci...267.1010G. doi:10.1126/science.267.5200.1010. See also Description on the researcher's website.
- ^ "Fractional charge carriers discovered". Physics World. 24 October 1997. http://physicsworld.com/cws/article/news/3393. Retrieved 2010-02-08.
- ^ R. de-Picciotto, M. Reznikov, M. Heiblum, V. Umansky, G. Bunin, D. Mahalu (1997). "Direct observation of a fractional charge". Nature 389 (6647): 162. Bibcode 1997Natur.389..162D. doi:10.1038/38241.
- ^ J. Martin, S. Ilani, B. Verdene, J. Smet, V. Umansky, D. Mahalu, D. Schuh, G. Abstreiter, A. Yacoby, (2004). "Localization of Fractionally Charged Quasi Particles". Science 305 (5686): 980–3. Bibcode 2004Sci...305..980M. doi:10.1126/science.1099950. PMID 15310895.
- ^ González-Martín, Gustavo R. (1991). "Some electromagnetic consequences of a unified theory of gravitation and electromagnetism". Gen. Rel. And Grav. 23 (7): 827. Bibcode 1991GReGr..23..827G. doi:10.1007/BF00755997. http://www.springerlink.com/content/h4j801591u83h514/.
- ^ González-Martín, Gustavo R. (1997). "Charge to magnetic flux ratios". ArXiv: cond–mat/0009181. http://arxiv.org/ftp/cond-mat/papers/0009/0009181.pdf.
References
- D.C. Tsui, H.L. Stormer, A.C. Gossard (1982). "Two-Dimensional Magnetotransport in the Extreme Quantum Limit". Physical Review Letters 48 (22): 1559. Bibcode 1982PhRvL..48.1559T. doi:10.1103/PhysRevLett.48.1559.
- H.L. Stormer (1999). "Nobel Lecture: The fractional quantum Hall effect". Reviews of Modern Physics 71 (4): 875. Bibcode 1999RvMP...71..875S. doi:10.1103/RevModPhys.71.875.
- R.B. Laughlin (1983). "Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations". Physical Review Letters 50 (18): 1395. Bibcode 1983PhRvL..50.1395L. doi:10.1103/PhysRevLett.50.1395.